RF-dressed Potentials
Schumm, T., Hofferberth, S., Andersson, L.M., Wildermuth, S., Groth, S., Bar-Joseph, I., Schmiedmayer, J. & Krüger, P.
Matter wave interferometry in a double well on an atom chip
Nature Phys., 2005, Vol. 1, pp. 57-62
Hofferberth, S., Fischer, B., Schumm, T., Schmiedmayer, J. & Lesanovsky, I.
Ultracold atoms in radio-frequency dressed potentials beyond the rotating-wave approximation
Physical Review A, 2007, Vol. 76(1), pp. 013401
A one-dimensional Bose-Einstein condensate trapped in a tight magnetic trap can be split into two by means of an adiabatic radio frequency induced potential. By interfering the condensates we show that the splitting process preserves the relative phase between the two BECs even when they are split far enough to inhibit tunnel coupling.
At the centre of our interference experiments is the beam splitter. It is based on radio frequency induced adiabatic potentials. This technique has the advantage of allowing a smooth transition from a single trap into a double well potential and hence coherent splitting is possible. In contrast to other methods, the splitting distance can be orders of magnitude smaller than the chip structures. We precisely control the splitting of condensates over a range from 3-80 µm. Our new technique allows to construct versatile chip based atom interferometers. Our scheme is based on a combination of static and radio frequency (RF) magnetic fields. The beam splitter is fully integrated on the atom chip, as these fields are provided by microfabricated wires. By slowly changing the parameters of the RF current we can smoothly transform a tight magnetic trap into a double well and thereby dynamically split a BEC. We accurately control the splitting distance over a wide range. The potential barrier between the two wells can be raised gradually with high precision, thus enabling access to the tunnelling regime as well as to the regime of entirely isolated wells. We complete an interferometer sequence and measure the relative phase between the split BECs by recombining the clouds in time-of-flight expansion. In our experiments we find an interference pattern with a fixed phase as long as the two wells are not completely separated. The phase starts to evolve deterministically once the wells are entirely separated so that tunnelling is fully inhibited on all experimental time scales. The figure on the below side illustrates the operation principle of the beam splitter. A standard magnetic microtrap is formed by passing a current through a wire. In combination with an external bias field a static magnetic field minimum forms where atoms in low field seeking states can be trapped. An additional RF field generated by an independent wire carrying an alternating current couples internal atomicby the dressed eigenstates. In our scheme we are able to form a three dimensionally confining trap with a double well shape in one of the transverse strongly confined directions. Here it is relevant that not only intensity and frequency, but also the orientation of the RF field determine the effective potential. The angle between the RF field and the local static magnetic field varies spatially, resulting in a corresponding variation of the RF coupling strength.Our smooth micro wires enable us to create pure quasi one-dimensional condensates (aspect ratio 400) with chemical potential µ ~ hω⊥ in a trap with high transverse confinement (ω⊥ = 2 · 2.1 kHz). These BECs are located directly above an auxiliary wire. A small sinusoidally alternating current through this wire provides the RF field that splits the trap. For small splitting distances (< 6 µm) we ramp the amplitude of the RF current (typically 60-70 mA) at a constant RF frequency (~ 500 kHz) to smoothly split a BEC confined in the single well trap into two. The splitting is performed transversely to the long axis of the trap, as shown in the figure (b). The distance between the two wells can be further increased by additionally raising the frequency of the RF field (up to 4 MHz).
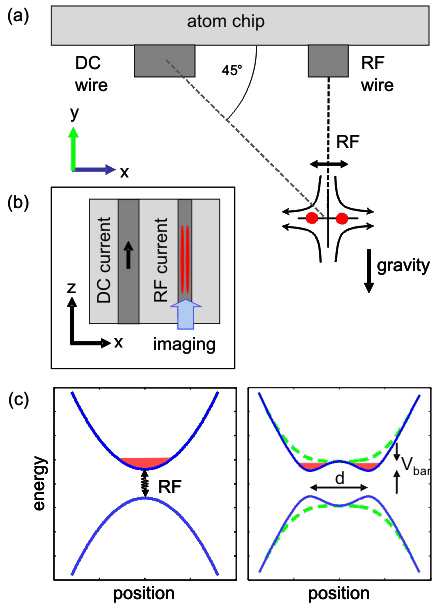(a) A straight wire carrying a static (DC) current (~ 1A) is used to trap a BEC on an atom chip directly above a second wire carrying a radio frequency (RF) current (~ 60 mA at 500 kHz). Placing the trap at the indicated position allows symmetric horizontal splitting. (b) Top view onto the atom chip (mounted upside down in the experiment): An elongated BEC is transversely split. All experimental images are taken along the direction parallel to the wires. (c) Left: The RF magnetic field couples different atomic spin states (only two shown for simplicity). Right: An RF frequency below the Larmor frequency at the trap minimum (~ 1 G) only relaxes the trapping potential in both transverse directions (dashed line) as long as the orientation of the RF field is orthogonal to the trapping field. An RF field oriented along x breaks the rotational symmetry of the trap, as its angle with the local static field varies along x, while along y this angle is always 90°. This leads to a spatially varying coupling strength which can be exploited to form a double well potential along x (solid blue line) while there is no splitting along y (dashed green line). By adjusting the RF amplitude and/or frequency, a single well can smoothly (adiabatically) be transformed into a double well allowing for coherent splitting of a condensate. Double well potentials can be formed both for RF frequencies below and above the Larmor frequency.The split cloud is detected by in situ absorption imaging along the weak trapping direction. We are able to split BECs over distances of up to 80 µm without significant loss or heating. The measured splitting distances are in very good agreement with the theoretical expectation for different gradients of the initial single well (figure below).The splitting distances are not limited by the structure size on the chip, but rather by the ground state size of the initial single well trap that can be orders of magnitude smaller. This allows us to reach full splitting of a BEC at a double well separation of only 3.4 µm using a trapping wire of a width of 50 µm at a distance of 80 µm from the surface. Furthermore, the dynamic splitting process can be performed in a smooth (adiabatic) fashion by simply controlling the parameters of the RF field. We recombine the split clouds in time-of-flight expansion after a non-adiabatically fast extinction of the double well potential. Typical matter wave interference patterns obtained by taking absorption images 14 ms after releasing the clouds are. The integrated transverse density profile derived from these images contains information on both the distance d of the BECs in the double well potential and the relative phase Φ of the two condensates. The figure below shows the observed fringe spacing that is compared to the above approximation and to a numerical integration of the timedependent Gross-Pitaevskii equation. Again, we find excellent agreement.
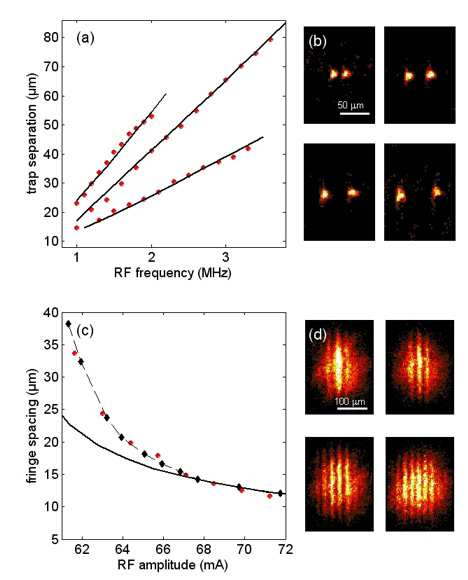(a) A comparison of the measured splitting distances (red circles) to the theoretical expectation (black lines) yields good agreement for three different trap configurations. (b) The experimental data is derived from in situ absorption images. (d) For distances below our imaging resolution (d < 6µm), we derive the splitting distances from interference patterns obtained after 14 ms potential-free time-of-flight expansion of the two BECs. (c) The fringe spacing is plotted as a function of RF amplitude (red circles). A simple approximation of the expected fringe spacing based on an expansion of a non-interacting gas from two points located at the two minima of the double well potential agrees well with the data for sufficiently large splittings (solid line). For small splitting distances (large fringe spacing), inter-atomic interactions affect the expansion of the cloud. A numerical integration of the time-dependent Gross-Pitaevskii equation using our experimental parameters takes this effect into account (black diamonds). We find good agreement to this theory. The original single well trap had a transverse oscillation frequency of 2π· 2.1 kHz.The observed differential phases ΔΦ in the interference patterns are nonrandom. Hence, the splitting process is phase preserving and coherence is maintained. The differential phase spread ΔΦ is smaller than 50° for splittings of up to 3.7µm (figure below). When separating the clouds further, the phase distribution remains nonrandom
up to at least d = 6µm. An increase in phase spread and a coinciding loss of average contrast can be attributed to longitudinal phase diffusion inside the individual one-dimensional quasi BECs. Determining the phase distribution at different stages of the splitting procedure, we observe that the relative phase is locked to zero, as long as the chemical potential exceeds the potential barrier; for trap separations larger than 3.4µm, the potential barrier is sufficiently high to suppress tunnelling. We observe a deterministic phaseshift after the splitting is complete. This differential phase evolution is induced by a slight residual imbalance of the double well potential (energy difference on the order of h · 1 kHz or, equivalently, µB · 1 mG).
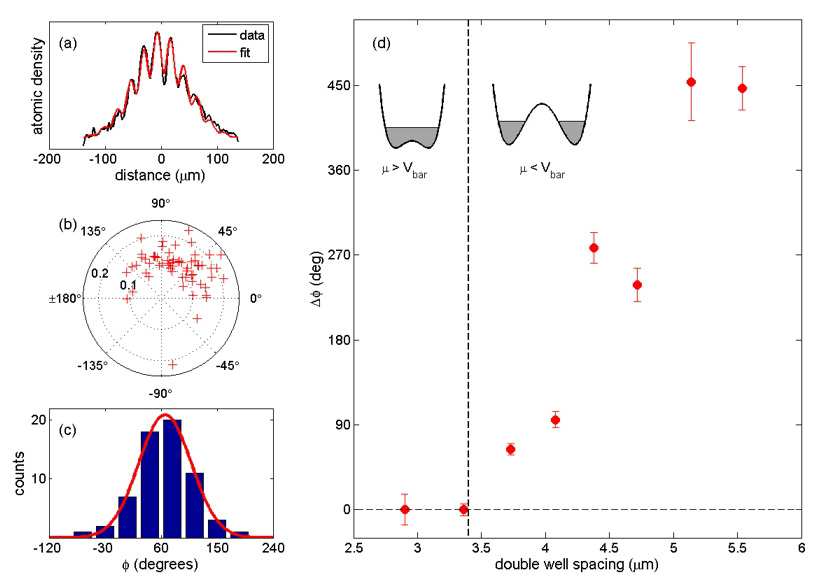(a) A cosine function with a Gaussian envelope is fitted to the obtained profiles yielding information on fringe spacing, contrast, and phase. (b) Contrast and phase for 82realizations of the same experiment are plotted in a polar diagram for a double well splitting of 3.7µm. (c) A histogram of the measured differential phase shows a Gaussian distribution around a phase shift of 66°. The barrier between the wells suppresses tunnel coupling completely. The width of the distribution (σ = 46°) is significantly narrower than for a random phase. (d) Phase evolution during the splitting process (error bars indicate the statistical error of the mean of the distribution). The dashed vertical line indicates the splitting distance at which the chemical potential m of the BEC is equal to the potential barrier height Vbar. As long as the barrier between the two wells is too low to prevent tunnel coupling (to the left of the dashed line), the relative phase remains locked at zero. Once the wells are fully separated (to the right of the dashed line), the differential phase starts to evolve due to a residual slight imbalance in the double well potential. The clouds were split at a rate of ~ 2µm/ms. Phase diffusion within the quasi one-dimensional BECs used in our experiments is predicted to occur on the same timescale this explains a reduction of contrast and increasing phase spread as the splitting distance is increased.
Write a comment