Optimal control of BECs

Robert Bücker, Tarik Berrada, Sandrine van Frank, Jean-François Schaff, Thorsten Schumm, Jörg Schmiedmayer, Georg Jäger, Julian Grond, and Ulrich Hohenester.
Vibrational State Inversion of a Bose–Einstein Condensate: Optimal Control and State Tomography.
Journal of Physics B 46 (2013): 104012.

Bose-Einstein condensates (BEC) are today among the most precisely controllable and observable many-body quantum systems. Spectacular progress has been made in preparing complex quantum states of a BEC, ranging from the implementation of condensed-matter theory models to highly entangled states akin to quantum optics experiments. The time and length scales accessible in such experiments allow both to precisely detect the quantum state reached, and to observe its dynamics in response to external driving or while relaxing from an out-of-equilibrium situation.

These assets qualify BECs as an excellent model system to explore strategies of quantum control, such as quantum optimal control theory (OCT), in a many-body setting. OCT provides a theory framework for optimizing speed and fidelity of quantum state manipulation, which has already been successfully applied in various fields of physics, such as pulse shaping in NMR spectroscopy and control of chemical reactions. Applications of OCT on BECs so far have focused on “shortcuts to adiabaticity”, where the system remains in its ground state even under fast parameter changes.

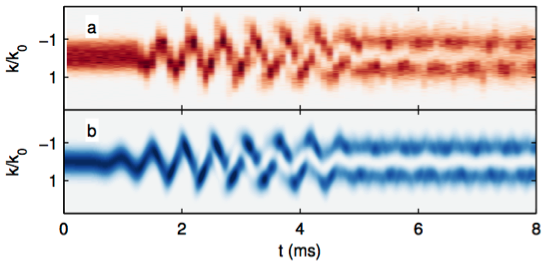
In collaboration with the Hohenester group at the University of Graz, we have now applied OCT to condensates in a rather different way, namely, to precisely steer the collective wave function of a BEC into a highly out-of-equilibrium quantum state. As published in J. Phys. B, a protocol was derived to realize a “population inversion” into an excited vibrational state of a trapped BEC, which is essentially a many-body version of a harmonic oscillator eigenstate, that has no classical counterpart (see figure).

Unlike more conventional techniques for changing the wave function of a trapped system, such as sideband transitions, the transfer is achieved solely by applying a “shaking” force on the BEC, moving the confining potential in a controlled way. Using the experimental approach of trapping condensates by means of currents on microchips (atom chips), which inherently allows for fast trap modulations, no further experimental tools are required for the state transfer. The time-dependent momentum distribution of the condensate is imaged; comparison to numerical results shows excellent agreement (see figure), and a near-unit fidelity of the process is demonstrated within a time corresponding to only a few oscillations in the confining potential. Furthermore, it is shown, how the complex driven dynamics of the wave function can be approximated by an intuitive two-level description.

The inverted state has already been used as a source for parametric amplification of quantum-correlated twin-atom beams. In the future, OCT techniques should allow accessing a much larger class of complex many-body states, such as squeezed and entangled states. Moreover, by implementing not only transitions between states, but rather any quantum operation in general, e.g. vibrational state interferometers seem now within reach.

Measured (a) and calculated (b) dynamics of the condensate momentum distribution, where each column corresponds to a measured time step.