One-dimensional Bose Gases
1d-condensates in microtraps
One-dimensional systems are usually realized in cylindrically symmetric traps offering strong confinement in the transverse direction and weak confinement along the longitudinal direction. If the relevant energy scale of a thermal cloud (kBT) or a Bose-Einstein condensate (chemical potential µ) becomes smaller than the energy hωtrans associated with the transverse level-spacing, excitations in this direction are frozen out.
Zero temperature and weakly interacting regime:
The different possible regimes for a 1d-system at zero temperature are sketched in the figure below. The experiments are performed at α~1 and probe the weakly interacting Thomas-Fermi regime. For α<<1 the strongly interacting regime is absent for any atom number N since the harmonic confinement of the trap rather than interactions governs the motion of particles. If N >> α-1 the condensate forms in the one-dimensional Thomas-Fermi regime where the chemical potential is µ >> ωlo. Reducing the atom number leads to a reduction of the mean-field interaction which, at some point, becomes smaller than the longitudinal level spacing ωlo in the trap. This leads to a macroscopic occupation of the ground state of the trap yielding an ideal gas condensate with a Gaussian shape.
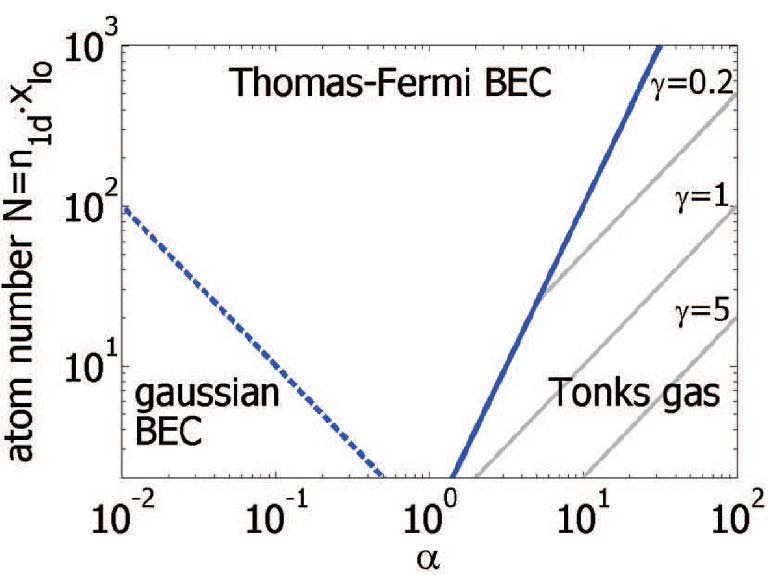 Depending on the parameter a and N different states for trapped one-dimensional gases are possible. This diagram has been plotted following. The dashed (solid) blue line indicates the cross-over region between a Thomas-Fermi BEC and a gaussian BEC.
Depending on the parameter a and N different states for trapped one-dimensional gases are possible. This diagram has been plotted following. The dashed (solid) blue line indicates the cross-over region between a Thomas-Fermi BEC and a gaussian BEC.Finite temperature and weakly interacting regime:
In the experimentally much more easily accessible regime of small α and large N (or N > α2) one always has got a weakly interacting gas. This 1d-regime is characterized by the longitudinal phase coherence length Rph of a condensate. The phase of the condensate is only coherent over a certain length which is smaller than the longitudinal size of the system. This means that the phase coherence length Rph is smaller than the longitudinal length of the condensate. Note, that the transition between the three possible states for a 1d-bose gas (true-condensate, quasi-condensate, and Tonks gas) is smooth. The cross-over region between true-condensate and quasi-condensate is depicted in the figure below as a solid line.
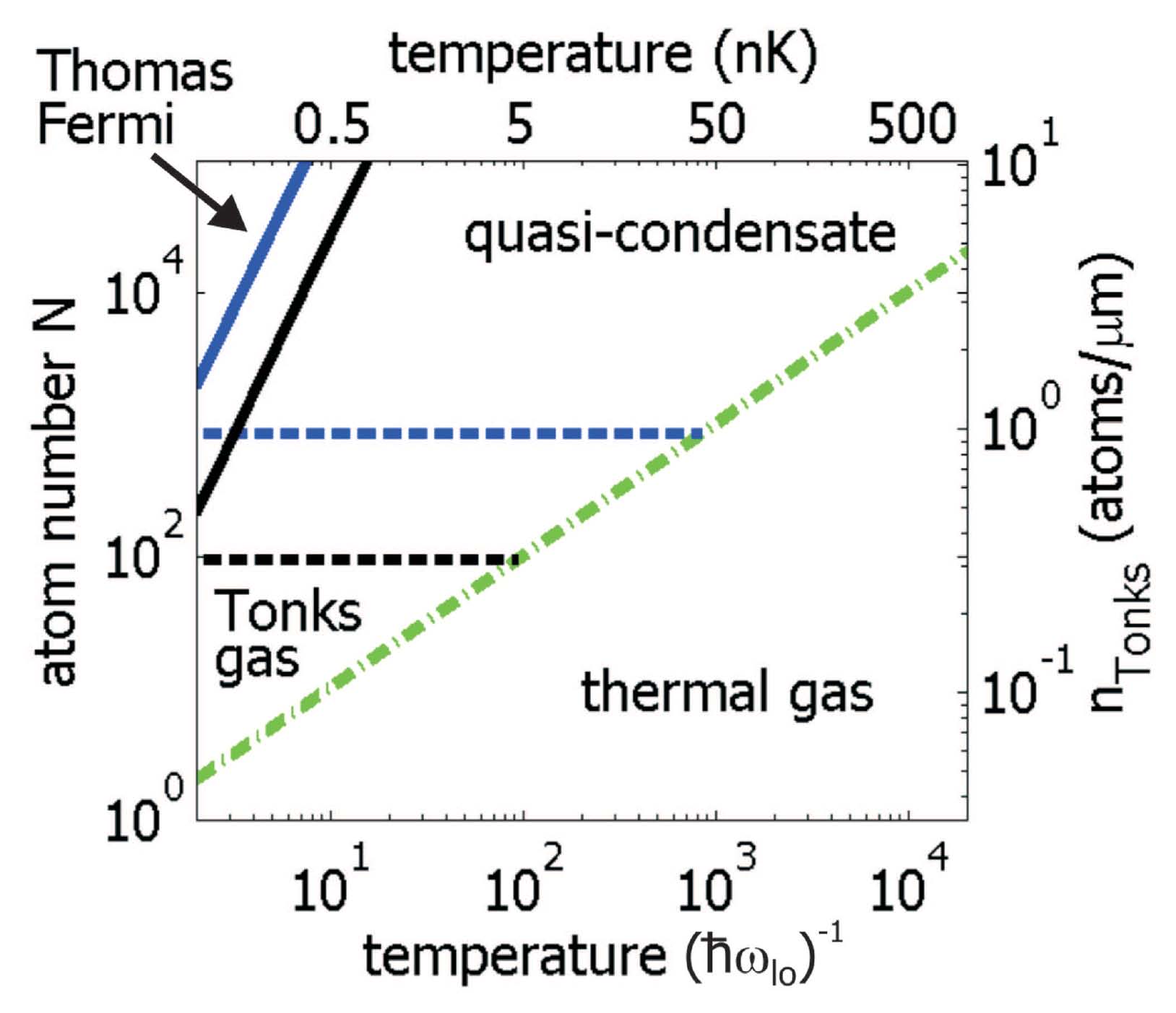 For sufficiently low T the quantum degenerated regime in entered (green line) where three states are possible. The blue (black) curve corresponds to α = 30 (α = 10).
For sufficiently low T the quantum degenerated regime in entered (green line) where three states are possible. The blue (black) curve corresponds to α = 30 (α = 10).Cross-over between 1d and 3d BEC:
Cross-over between 1d and 3d BEC: In our setup it is possible to probe the entire cross- over region down to longitudinal 1d-densities of 13atoms/µm. This is a factor 15 smaller than the limit given by 1/a3D. The transverse size for an expanded BEC prepared at different longitudinal densities shows good agreement with theory and a two-dimensional GPE simulation. Moreover the exact shape of the expanded BEC has been probed in detail and the continuous evolution from a gaussian shape to a parabolic shape has clearly been observed.
The figure below shows an absorption image of a disordered BEC after 5ms of ballistic expansion. The BEC has been formed at a distance of 10µm above the 100µm-wide Z-shaped wire at a current of 340mA, resulting in ωtrans = 2π · 3.5kHz. The longitudinal 1d-density n1d has been calculated and clearly fulfills n1d < 190atoms/µm. In the logarithmic plot it can be seen that the BEC stretches almost continuous over the entire length of 1mm. The detection sensitivity can be estimated from this longitudinal profile to be >> 4atoms/µm. This profile derived after time-of-flight expansion has been compared to a profile taken by in-situ imaging. The longitudinal structure of the trapped BEC has been found to be the same as the expanded one. For each width the corresponding longitudinal 1d-density n1d has been taken. To probe higher densities a BEC has been formed at a distance of 50µm from the chip surface where a homogeneous longitudinal profile is obtained. In figure below the average over 20 absorption pictures of an expanded one-dimensional quasi-BEC can be seen. This BEC has been generated in a trap with ωtrans = 2π · 2.9kHz and ωlong = 2π·8Hz and has been imaged after 22ms of ballistic expansion. In the longitudinal 1d-density profile depicted one clearly sees a small thermal component which has been fitted by a gaussian distribution (black dashed curve). The resulting width and amplitude have been used to simulate an isotropic 2d-thermal distribution. As a result the pure distribution of the BEC component is obtained. Small residual fluctuation at the outer parts of the distribution can be estimated to be smaller than 10atoms/µm. Expansion in the longitudinal direction of a BEC from such a trap is smaller than the resolution of the imaging system. The same longitudinal profile has been found. Therefore the transverse width of the BEC at every single longitudinal position can be linked to the local 1d-density. For high densities these profiles deviate from the Gaussian shape but still have been fitted by a gaussian distribution to avoid any bias when extracting the width. The Gaussian test function underestimates the actual width of the distribution by a few percent.
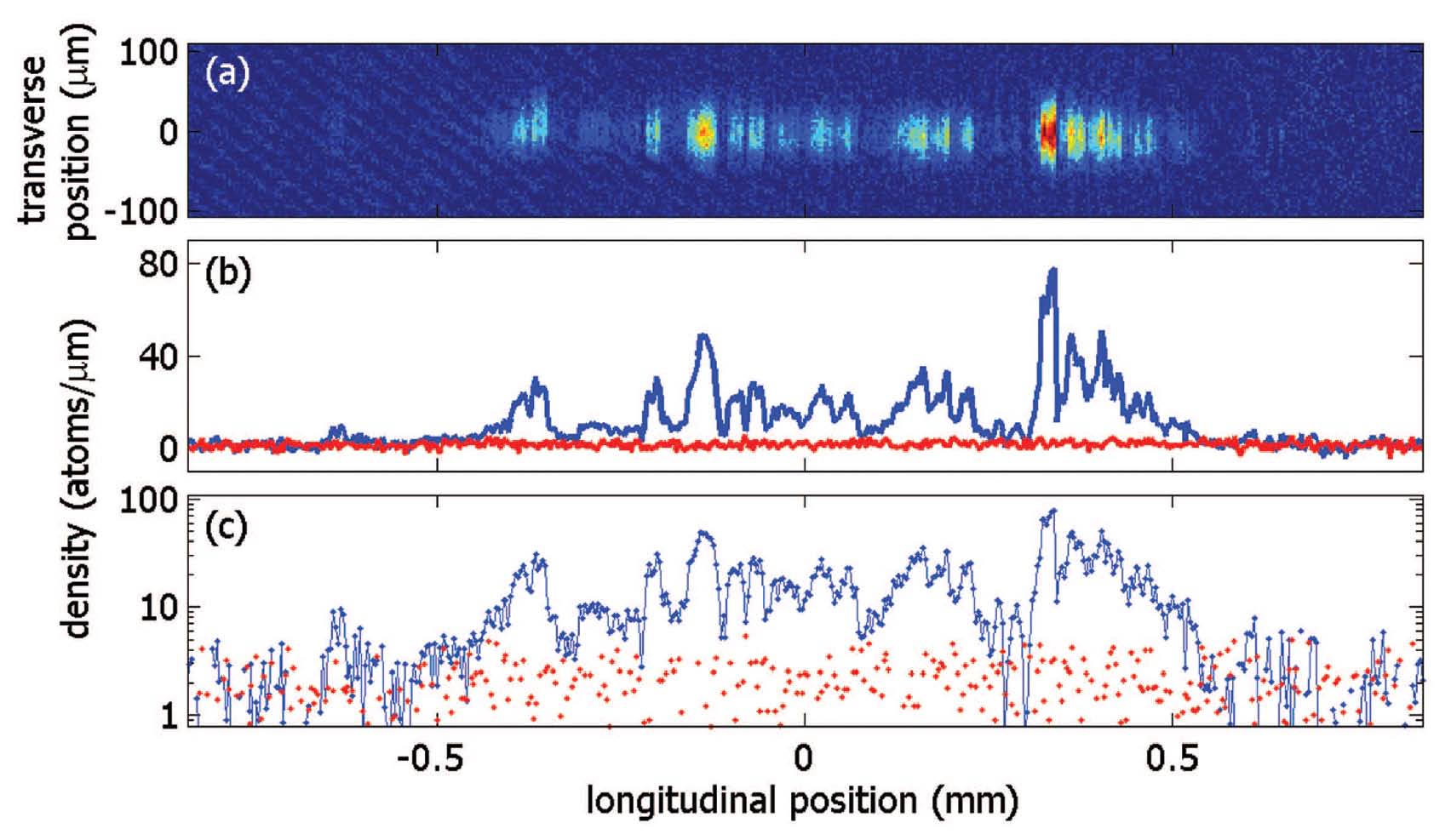 (a) Absorption image of a fragmented BEC taken after 5ms of time-of-flight expansion.The BEC has been formed at a distance of 10µm from the wire surface. (b) Longitudinal one-dimensional density profile (blue) derived from the absorption picture. The noise-level is shown in red. (c) To accentuate the noise-floor of ~ 4 atoms/µm the same data has been plotted logarithmic. A continuous BEC stretches over a length of more than 1mm.
(a) Absorption image of a fragmented BEC taken after 5ms of time-of-flight expansion.The BEC has been formed at a distance of 10µm from the wire surface. (b) Longitudinal one-dimensional density profile (blue) derived from the absorption picture. The noise-level is shown in red. (c) To accentuate the noise-floor of ~ 4 atoms/µm the same data has been plotted logarithmic. A continuous BEC stretches over a length of more than 1mm. 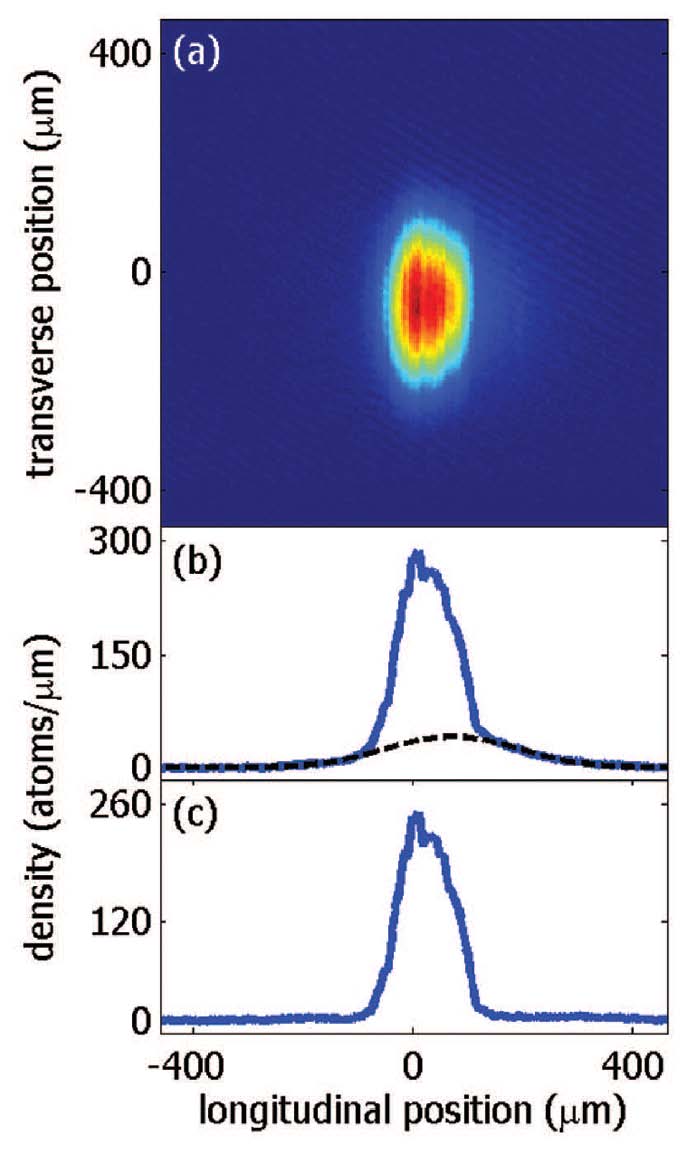 (a) Average over 20 absorption pictures of an expanded 1D quasi-BEC created at a distance of 50µm. (b) The longitudinal 1d-density profile shows a small thermal component which has been fitted by a Gaussian (black dashed line). The resulting width and the amplitude have been used to generate a 2d-thermal distribution which has been subtracted from the image. (c) The width of the thermal component after 22ms of ballistic expansion yields a temperature of 373+-9 nK. The asymmetry is cause by a small gradient due to gravity.
(a) Average over 20 absorption pictures of an expanded 1D quasi-BEC created at a distance of 50µm. (b) The longitudinal 1d-density profile shows a small thermal component which has been fitted by a Gaussian (black dashed line). The resulting width and the amplitude have been used to generate a 2d-thermal distribution which has been subtracted from the image. (c) The width of the thermal component after 22ms of ballistic expansion yields a temperature of 373+-9 nK. The asymmetry is cause by a small gradient due to gravity.